Bloom Filter

Bloom Filter is a data structure that allows rapid lookup on an element, say a string whether it is present in a set. Implementation-wise, it is a bit vector that contains an array of zeros and ones (booleans) with a fixed length. It is known for its space and time efficiency.

It is probabilistic in nature that is useful for lookup on non-critical data, such as caching search keywords and detecting weak passwords. Upon querying, bloom filter will only return one of the two responses - "maybe" or "no".

If the answer is "maybe", there is a high possibility that the data is indeed there, based on the allowed false positive rate configured. If the answer is "no", then the data is definitely absent in the set. In other words, a Bloom Filter can have a low chance of getting a False positive (Type I Error) but never a False negative.

Here is a simple Bloom Filter with the size of 10 for demonstration.

How it works

To add an item in the Bloom Filter, it takes the input and hashed it with a few hash functions to get multiple hash digests. Subsequently, the results are used to determine the position of the bits to be flipped.

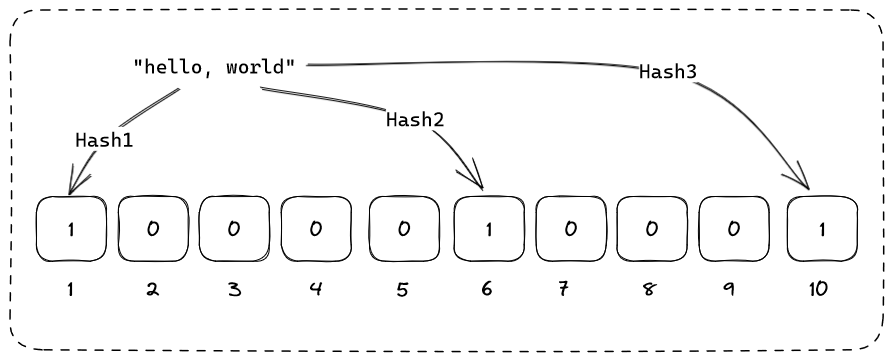
Here, we take the string "hello, world" and hash it with 3 different, independent hash functions and flip the bits accordingly.

After that, when a query tries to lookup for the same value, the hash produced will be the same and the results will points to the same bits that is already flipped, indicating the item is very likely to be there.

Let's try to query for the string "hi, mum" and observe the behaviour.

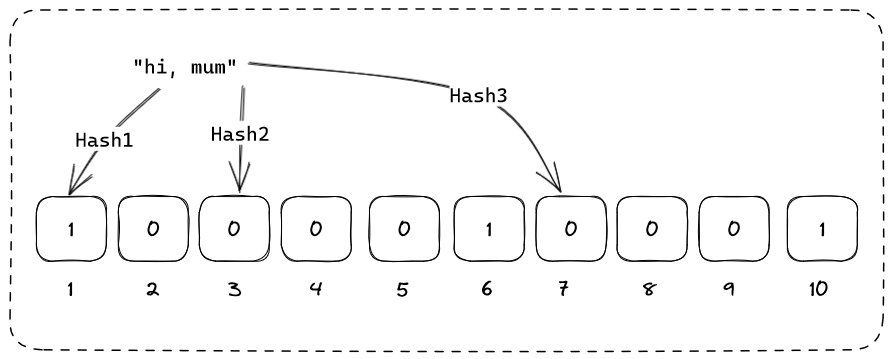
Base on the results, only Hash1 got a match whereas both Hash2 and Hash3 did not. Hence, we can deduce that "hi, mum" definitely does not exist.

Collision

As the number of items in the Bloom Filter increases, more bits are being flipped and collision are bound to happen. Given a non-existing input, all of the hash functions may even have their results point to the flipped bit, hence producing a false positive result and this is the reason bloom filter is considered as a probabilistic data structure.

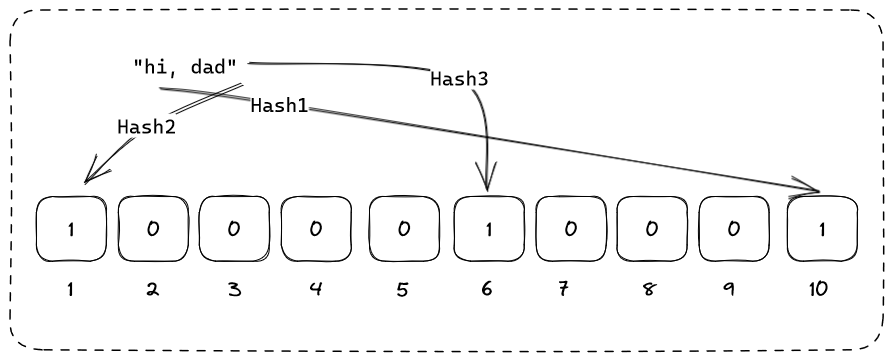
The hashes for the string "hi, dad" coincidentally fall to the flipped bits by "hello, world" earlier and this shows how a false positive can manifest.

The good news is, with proper tuning of the parameters, we can minimize the rate of false positivity to the threshold that is low enough to be acceptable for our use case.

Parameters

Here are the parameters that can be controlled.

	Parameter	Description
1.	Bit array,	The size of the bloom filter
2.	Hash function,	The number of hash function used
3.	Items in filter,	Total amount of items inserted
4.	False positive probability,	The rate of getting false positive

The relationships between the parameters can be represented by the formula as follows.

As the probability of false positive is directly proportional to the number of items inserted, we would like to fix to be the maximum amount of items that we want to insert instead. This way, we can achieve a fixed maximum and whats left to determine is the size of the bit array, .

The number of hash function, can either be set arbitrary or by calculation.

However, be mindful that the number of hash functions used does not correspond to the efficiency of the Bloom Filter as it will occupy more bits when inserting an element and consequently increases the likelihood of a collision. In fact, the more hash functions used, the slower it is for the operation to execute.

Sample Implementation

This is a simple implementation in JavaScript. For Python's implementation, refer to Brilliant.org.

var crypto = require('crypto')

class BloomFilter {
  #size
  #sliceStart
  #sliceEnd
  #array
  #itemCount = 0

  get itemsAdded() {
    return this.#itemCount
  }

  constructor(size = 50, sliceStart = 0, sliceEnd = 4) {
    this.#size = size
    this.#sliceStart = sliceStart
    this.#sliceEnd = sliceEnd
    this.#array = new Array(size)
  }

  insert(string) {
    var [hash1, hash2, hash3, hash4] = this.#getHashes(string)

    this.#array[
      Number('0x' + hash1.slice(this.#sliceStart, this.#sliceEnd)) % this.#size
    ] = 1
    this.#array[
      Number('0x' + hash2.slice(this.#sliceStart, this.#sliceEnd)) % this.#size
    ] = 1
    this.#array[
      Number('0x' + hash3.slice(this.#sliceStart, this.#sliceEnd)) % this.#size
    ] = 1
    this.#array[
      Number('0x' + hash4.slice(this.#sliceStart, this.#sliceEnd)) % this.#size
    ] = 1
    this.#itemCount++
  }

  find(string) {
    var [hash1, hash2, hash3, hash4] = this.#getHashes(string)

    return !!(
      this.#array[
        Number('0x' + hash1.slice(this.#sliceStart, this.#sliceEnd)) %
          this.#size
      ] &&
      this.#array[
        Number('0x' + hash2.slice(this.#sliceStart, this.#sliceEnd)) %
          this.#size
      ] &&
      this.#array[
        Number('0x' + hash3.slice(this.#sliceStart, this.#sliceEnd)) %
          this.#size
      ] &&
      this.#array[
        Number('0x' + hash4.slice(this.#sliceStart, this.#sliceEnd)) %
          this.#size
      ]
    )
  }

  showState() {
    console.log('State are as follows: ', this.#array)
  }

  #getHashes(str) {
    var hash1 = crypto.createHash('sha1').update(str).digest('hex')
    var hash2 = crypto.createHash('sha256').update(str).digest('hex')
    var hash3 = crypto.createHash('mdc2').update(str).digest('hex')
    var hash4 = crypto.createHash('sha384').update(str).digest('hex')

    return [hash1, hash2, hash3, hash4]
  }
}

Strings can be inserted via the insert method, find for the lookup operation that returns a boolean value and the showState method shows the current state of the bit array. The #itemCount keep tracks of how many elements has been inserted since its instantiation.

The #sliceStart and #sliceEnd does not have anything to do with Bloom Filter. It is just a way I personally use to interpret the hashes and convert them into bit array positions.

Closing Remark

In short, Bloom Filter is a powerful and efficient data structure that can be used in situations when false positive can be tolerated. By tolerating the slim chance of collision, we are rewarded with an incredibly memory efficient data structure with miniscule size.

How it works

Collision

Parameters

Sample Implementation

Closing Remark

Reference